畳み込みニューラルネットワークの勉強のまとめ その3

前回の多クラス分類に続き、今回は多層ネットワークとその学習について説明します。

(いろいろ別の作業が入ってしまって、遅くなりました…)

多層ネットワーク

今回の多層ネットワークでは、下の図のような構成となります。

（重み付け和と活性化関数の表示は省略…）

入力層と出力層の間に中間層を挟み、入力層から中間層、中間層から出力層へとそれぞれの間で重み付け和と活性化関数による演算を行います。

前段（入力層から中間層）の計算は、活性化関数を\(f^{(1)}(\cdot)\)とすると

\[z_j = f^{(1)} (a_j^{(1)}) = f^{(1)} \left( \sum_i x_i w_{ij}^{(1)} + b_j^{(1)} \right) \tag{1}\]

同様に後段（中間層から出力層）の計算は、活性化関数を\(f^{(2)}(\cdot)\)とすると

\[y_k = f^{(2)} (a_k^{(2)}) = f^{(2)} \left( \sum_j z_j w_{jk}^{(2)} + b_k^{(2)} \right) \tag{2}\]

となります*1。

まず最初に\( (2)\)式の後段に着目してみましょう。この後段の出力は各クラスの確率を表現できるように前回説明した多クラス分類を使います。ここで確率的勾配降下法を使って学習するとき、前回の\( (11)\)式と\( (12)\)式から

\[\frac{\partial E}{\partial w_{jk}} = (y_k - t_k) z_j \tag{3}\]

\[\frac{\partial E}{\partial b_k} = y_k - t_k \tag{4}\]

となり、これを使って

\[w_{jk} \leftarrow w_{jk} - \epsilon \frac{\partial E}{\partial w_{jk}} \tag{5}\]

\[b_k \leftarrow b_k - \epsilon \frac{\partial E}{\partial b_k} \tag{6}\]

として後段の重みとバイアスを更新して学習することになります。

ここで\( (3)\)式と\( (4)\)式の導出について、少し戻ってみてみましょう。\(\frac{\partial E}{\partial w_{jk}}\)と\(\frac{\partial E}{\partial b_k}\)それぞれに対して間に\(y_k\)と\(a_k^{(2)}\)による項を挟み込むと以下のように変形できていました。

\[\frac{\partial E}{\partial w_{jk}} = \frac{\partial E}{\partial y_k} \cdot \frac{\partial y_k}{\partial a_k^{(2)}} \cdot \frac{\partial a_k^{(2)}}{\partial w_{jk}} = \frac{\partial E}{\partial y_k} f^{'(2)} z_j \tag{7}\]

\[\frac{\partial E}{\partial b_k} = \frac{\partial E}{\partial y_k} \cdot \frac{\partial y_k}{\partial a_k^{(2)}} \cdot \frac{\partial a_k^{(2)}}{\partial b_k} = \frac{\partial E}{\partial y_k} f^{'(2)} \tag{8}\]

この\( (7)\)式および\( (8)\)式の意味するところは、

\[ \begin{align} \left[ \text{後段の重み更新用の値} \right] &= \left[ \text{後段の出力（出力層）による} E \text{の偏微}\text{分} \right] \\ &\qquad \times \left[ \text{後段の活性化関数の微}\text{分} \right] \\ &\qquad \times \left[ \text{後段の入力（中間層）}\right] \\ \left[ \text{後段のバイアス更新用の値} \right] &= \left[ \text{後段の出力（出力層）による} E \text{の偏微}\text{分} \right] \\ &\qquad \times \left[ \text{後段の活性化関数の微}\text{分} \right] \end{align} \]

となっています。

ひとまず後段はここまでにして、次に前段を見てみましょう。

前段の重み\(w_{ij}\)について考えてみます。\(E\)に対して重み\(w_{ij}\)で偏微分して\(\frac{\partial E}{\partial w_{ij}}\)を求めますが、\(E\)は\(y_k\)の関数であり、\( (2)\)式から\(y_k\)は\(z_j\)の関数なので、

\[\frac{\partial E}{\partial w_{ij}} = \frac{\partial E}{\partial z_j} \cdot \frac{\partial z_j}{\partial w_{ij}} \tag{9}\]

とできます。さらに\( (1)\)式から\(z_j\)は\(a_j^{(1)}\)の関数なので、

\[\frac{\partial E}{\partial w_{ij}} = \frac{\partial E}{\partial z_j} \cdot \frac{\partial z_j}{\partial a_j^{(1)}} \cdot \frac{\partial a_j^{(1)}}{\partial w_{ij}} = \frac{\partial E}{\partial z_j} f^{'(1)} x_i \tag{10}\]

同様にバイアスについても、

\[\frac{\partial E}{\partial b_j} = \frac{\partial E}{\partial z_j} f^{'(1)} \tag{11}\]

と求めることが出来、この\( (10)\)式と\( (11)\)式を使って

\[w_{ij} \leftarrow w_{ij} - \epsilon \frac{\partial E}{\partial w_{ij}} \tag{12}\]

\[b_j \leftarrow b_j - \epsilon \frac{\partial E}{\partial b_j} \tag{13}\]

として、前段の重みとバイアスを更新して学習できることになります。そして\( (10)\)式と\( (11)\)式の意味するところは、

\[ \begin{align} \left[ \text{前段の重み更新用の値} \right] &= \left[ \text{前段の出力（中間層）による} E \text{の偏微}\text{分} \right] \\ &\qquad \times \left[ \text{前段の活性化関数の微}\text{分} \right] \\ &\qquad \times \left[ \text{前段の入力（入力層）}\right] \\ \left[ \text{前段のバイアス更新用の値} \right] &= \left[ \text{前段の出力（中間層）による} E \text{の偏微}\text{分} \right] \\ &\qquad \times \left[ \text{前段の活性化関数の微}\text{分} \right] \end{align} \]

となって、後段と同じ形となります。まとめると、

\[ \begin{align} \left[ \text{重み更新用の値} \right] &= \left[ \text{同じ段の出力による} E \text{の偏微}\text{分} \right] \\ &\qquad \times \left[ \text{同じ段で使用した活性化関数の微}\text{分} \right] \\ &\qquad \times \left[ \text{同じ段の入力}\right] \\ \left[ \text{バイアス更新用の値} \right] &= \left[ \text{同じ段の出力による} E \text{の偏微}\text{分} \right] \\ &\qquad \times \left[ \text{同じ段で使用した活性化関数の微}\text{分} \right] \end{align} \]

と書けます。

このうち、活性化関数の微分は、例えばSigmoid関数であれば、

\[f^{'} = f ( 1 - f) = g(f) \tag{14}\]

というように、「元の活性化関数の出力」による関数に置き換えることが出来ます。

あと、\( (11)\)式でまだ求めていない\(\frac{\partial E}{\partial z_j}\)は、\( (7)\)式と同じように\( (2)\)式から

\[\frac{\partial E}{\partial z_j} = \frac{\partial E}{\partial y_k} \cdot \frac{\partial y_k}{\partial a_k^{(2)}} \cdot \frac{\partial a_k^{(2)}}{\partial z_j} = \frac{\partial E}{\partial y_k} f^{'(2)} w_{jk} \tag{15}\]

というように簡単に求めることが出来ます。

以上を図にすると次のようになります。

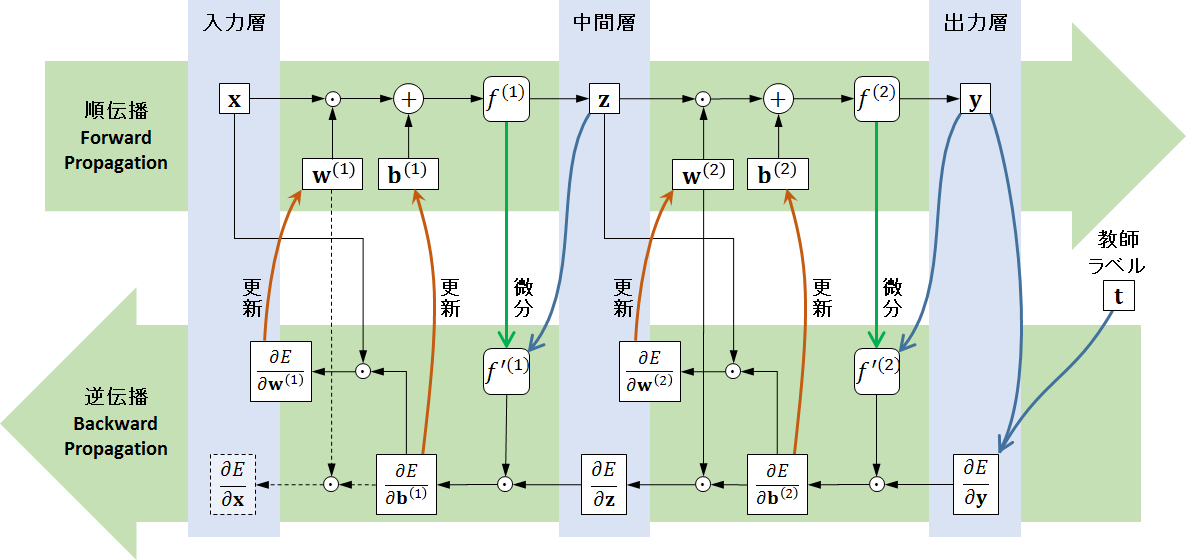
この図の下のように、データを入力を与えて得られた結果（出力）と教師ラベルによる誤差（っぽいもの）を入力方向（逆方向）へ伝播して学習（重み・バイアスを更新）していくので、これを誤差逆伝播法（Backpropagation）といいます。

次回は活性化関数についてもう少し詳しくみてみようと思います（たぶん）。

*1:重み\(\mathbf{w}\)は、各要素ごとにバラしました。